目次
  1. １．はじめに
  2. ２．風向データの修正
  3. ３．回帰係数と決定係数
  4. ４．注意点
  5. ５．具体例
  6. ５．おわりに

１．はじめに

風力開発を目的とした風況観測においては、観測マストでは観測が困難なサイトの風況を得るために、ドップラーライダー（Doppler LiDAR）に代表されるリモートセンシング機器の利用が急速に拡大しています。国内外の風況調査に関するガイドライン等1)2)3)4)には、リモートセンシング機器で計測した風向・風速の精度を定量的に評価する指標として、観測マストで計測した風向・風速を参照して得られる統計量（回帰係数と決定係数）が示されています。統計学における回帰係数と決定係数にはさまざまな定義があることが知られていますが、本稿ではガイドライン等1)2)3)4)を参照しながら、風況調査において用いられる統計量について、数式や具体例を示しながら解説していきます。

２．風向データの修正

風向は、風が吹いてくる方向として、0°から360°までの範囲の値を取りますが、各データをそのまま精度検証に使用すると、参照データ𝑥（例：観測マストのデータ）と対象データy（例：ドップラーライダーのデータ）の2次元上の位置関係から、図1に示すような直線y=xから大きく乖離するデータ（Raw data）が含まれる可能性があるため、統計量が正しく算出されません。そこで精度評価を行う前に、2つのデータが直線y=xに沿うように、以下に示すような修正を行います。

ここで、𝑥と𝑦の添字のi ( =1,2,3,…,N)は個のデータを示します。図1に示すように、修正によってRaw dataの代わりにModified dataが得られ、風向の統計量を正しく算出できるようになります。

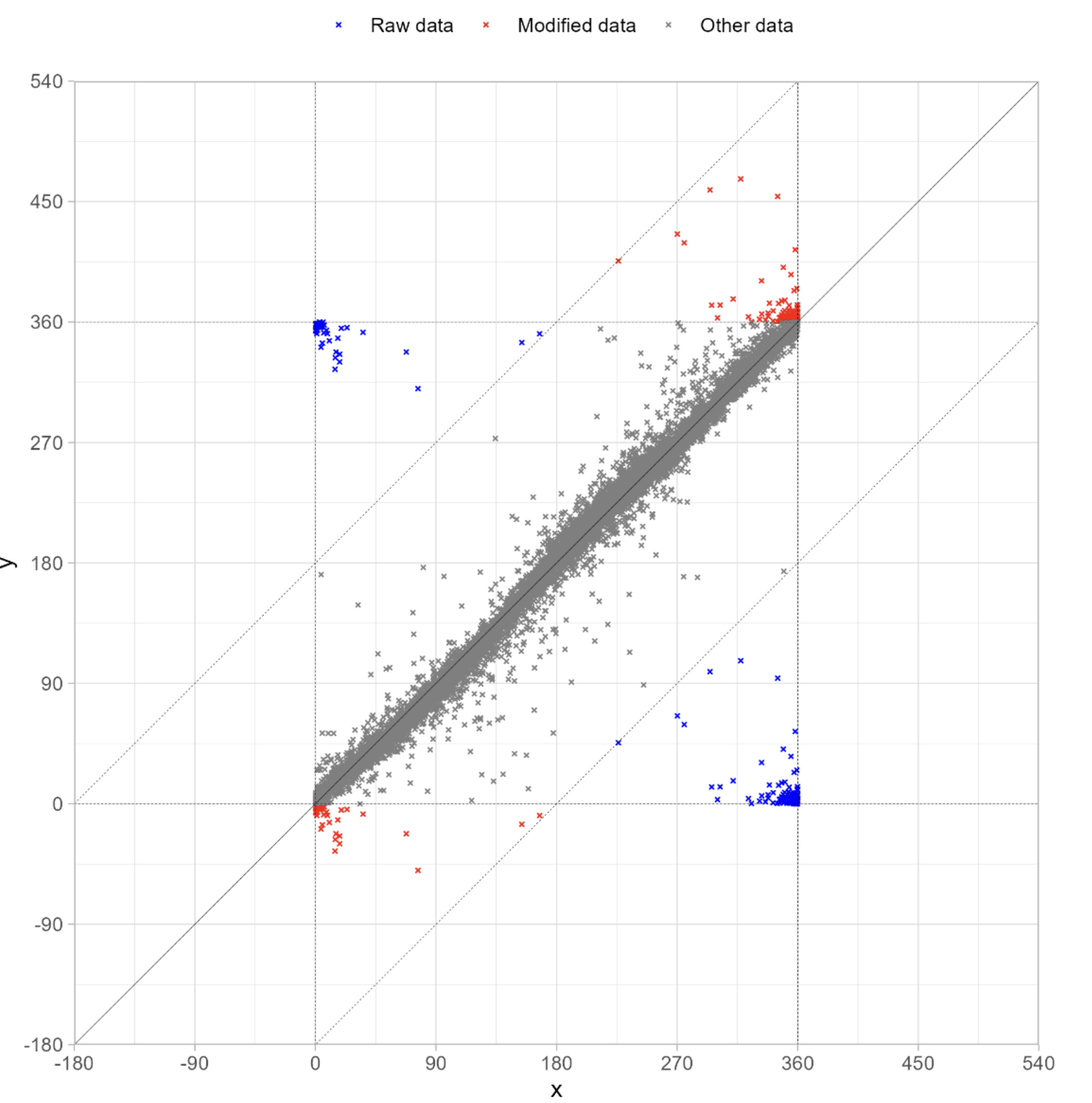
図1　風向データの操作

３．回帰係数と決定係数

リモートセンシング機器の風向・風速は、観測マストのデータ𝑥iを説明変数、リモートセンシング機器のデータyiを目的変数とした線形回帰によって評価されます。

風向の回帰直線は、切片ありのy= 𝑎𝑥+bとして表されます。その回帰直線の切片bは、Roadmap for the commercial acceptance of floating LIDAR technology1)の定義によると、𝑥iとyiの平均の差として次式で表されます。

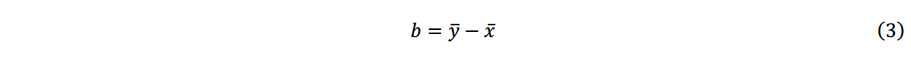
 ここで、𝑥 ̅は𝑥 iの平均値、y ̅はyiの平均値を示します。回帰直線の傾きaは切片bを通るように、最小二乗法に基づき次式で得られます。

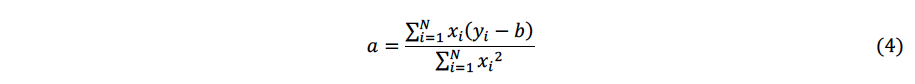
風速の回帰直線は、切片なしの𝑦 = 𝑎′𝑥として表されます。回帰直線の傾き𝑎は最小二乗法に基づき次式から求められます。

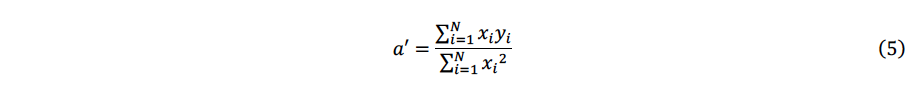
式(4)(5)に示すように、切片ありとなしの回帰係数の傾きはそれぞれ定義が異なります。

決定係数R2は、回帰直線がどの程度あてはまっているか、つまり、説明変数xがどの程度、目的変数yを説明しているかを表す指標です。Tarald O. Kvalseth5)は、R2について8つの定義（R21~R28）を示していますが、本稿ではそのうちの一般的な教科書6)などに掲載されているR21を次式に示します。

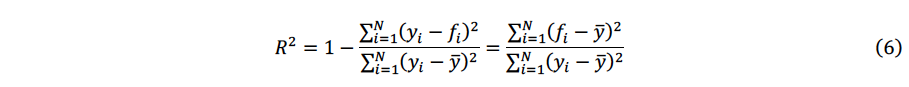
ここで、fiは回帰直線による推定値であり、風向であればfi= 𝑎𝑥i+b、風速であればfi= 𝑎′𝑥iとなります。R2は0から1の間の値をとり、R2=1のとき、𝑥iがyiを完全に説明しており、𝑥iとyiをグラフに描画すればすべての点が一直線上にのることを意味します。

４．注意点

実務上で統計量を算出する際には、表計算ソフト（Microsoft Excelなど）やプログラミング言語（python, R言語など）を使用する機会が多いのではないでしょうか。これらで実装されている回帰分析用の関数は、統計量の算出に非常に便利である反面、関数から導出される統計量がどのように定義されているのかをよく理解して使用する必要があります。

例えば、表計算ソフトやプログラミング言語で得られる回帰直線y= 𝑎𝑥+bの切片は、最小二乗法に基づく次式などで定義されているため、平均の差で定義される式(3)と一致しません。

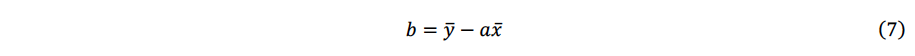
またR2については、表計算ソフト・プログラミング言語の違いや切片の有無によって式(6)と定義が異なることが指摘されており、具体的には、Excelで切片なしの回帰直線のR2を算出する場合にはR27が算出され、R21に比べて大きな値となることが確認されています7)8)。

したがって、表計算ソフトやプログラミング言語を用いて式(4)〜(6)に基づく統計量を算出する際には、回帰分析用の関数の代わりに、自作関数などを用いて定義に忠実なプログラムを構築することを推奨します。

５．具体例

精度検証の具体的な例として、ウィンドファーム認証 陸上風力発電所編2)（以下、NKガイドライン）と洋上風況観測ガイドブック4)に示される要求事項を紹介します。

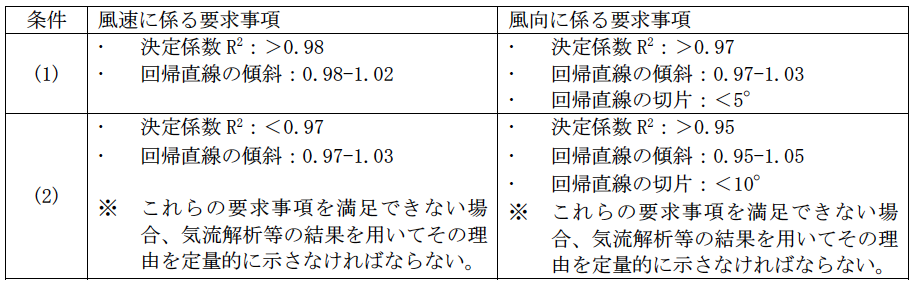
NKガイドラインでは、以下に示される条件(1)(2)に応じて、観測マストとリモートセンシング機器による観測データの相関を確認することが要求されています3)。

（1）観測マストとリモートセンシング機器による観測データを組み合わせることにより、ハブ高さでの観測データとして扱い、気流解析の入力データとする場合

（2）観測マストの観測データを気流解析の入力データとし、その気流解析の妥当性の検証用にのみリモートセンシング機器による観測データを用いる場合

表1 観測マストとリモートセンシング機器による観測データの相関3)

既往研究では、山間部のような複雑地形上でリモートセンシング機器により計測された風向・風速が、平坦地形上で計測されたものよりも精度が低下することが示唆されており9)10)、上記の要求事項を満足できないケースも生じることが想像されます（図2）。要求事項を満足できないときは、気流解析等の結果を用いてその理由を定量的に示す必要があります（表1）。これに関連して、気流解析結果を用いて、複雑地形におけるリモートセンシング機器のデータの誤差を補正する手法も検討されています11)12)。

図2　横軸を風況マスト、縦軸を鉛直ライダー（ベクトル平均）とした（左）風向と(右)風速の散布図9)

洋上風況観測ガイドブック4)では、風向と風速の精度のKPI（Key Performance Indicator; 重要評価指標）と許容基準が定義されています（表2）。リモートセンシング機器で計測した風向・風速の誤差が同表のミニマム以下である場合に、その計測値は観測マストのカップ形風速計または矢羽根形風向計と同等な精度を有するものとして利用することができると判断されます。ここで、風速範囲が4m/s以上16m/s未満とされているのは、発電量予測と風条件を算定する目的として、発電量や荷重への寄与が大きい範囲であると判断されているためです。

表2 精度のKPI及び許容基準

５．おわりに

本稿では、リモートセンシング機器で計測された風況データを評価するために使用される回帰係数と決定係数について解説しました。技術的な内容等ご不明点があれば、RTIへお気軽にお問い合わせください。

Reference
  1. Carbon Trust Offshore Wind Accelerator (OWA),Roadmap for the commercial acceptance of floating LIDAR technology, 2018, URL:
    https://www.carbontrust.com/our-work-and-impact/guides-reports-and-tools/roadmap-for-commercial-acceptance-of-floating-lidar,
    アクセス：2023/.
  2. 日本海事協会, ウィンドファーム認証 陸上風力発電所編, 2023,
    URL: https://www.classnk.or.jp/hp/pdf/authentication/renewableenergy/ja/windfarm/NKRE-GL-WFC01_March2023_Jpn_20230331.pdf,
    アクセス：2023/08/07
  3. ビューロベリタスジャパン, 登録適合性確認機関 適合性確認に係る技術基準, 2023, URL:
    https://www.bureauveritas.jp/sites/g/files/zypfnx696/files/media/document/windfirm_gijutsukijun_Rev0_0.pdf,
    アクセス：2023/08/07
  4. 新エネルギー・産業技術総合開発機構, 洋上風況観測ガイドブック, 2023, URL:
    https://www.nedo.go.jp/content/100948288.pdf,
    アクセス：2023/08/07
  5. Tarald O. Kvalseth, Cautionary Note about R2, The American Statistician Vol.39, No. 4, Part 1 (Nov., 1985), pp.279-285.
  6. 東京大学教養学部統計学教室, 統計学入門（基礎統計学Ⅰ）, 東京大学出版.
  7. 備忘ログ, Rのlmの決定係数R^2について定義式の違いでの差がどの程度なのかプロットしてみた, URL:
    https://indenkun.hatenablog.com/entry/2020/03/11/180921,
    アクセス：2023/08/07.
  8. 生物科学研究所 井口研究室, 決定係数 R2の違い: Excel, OpenOffice, LibreOffice および統計解析ソフト R を用いて, URL:
    https://biolab.sakura.ne.jp/r-squared.html,
    アクセス：2023/08/07.
  9. 水戸俊成，小長谷瑞木，加藤秀樹，嶋田進，田中久則，無電源地域や複雑地形におけるドップラーライダーを用いた風況観測の実績と課題，第41風力エネルギー利用シンポジウム予稿集, 2019, pp.199-202.
  10. 水戸俊成, 内山将吾, 見﨑豪之, 小長谷瑞木, 伊藤匠平, 複雑地形における鉛直型ドップラーライダーの観測精度に関する研究 (平均化による差異と補正手法の検討), 第43回風力エネルギー利用シンポジウム予稿集, 2021, pp.184-187.
  11. Meissner, C. and Boquet, M.: Correction of LiDAR remote sensing measurements by CFD simulations, in: EWEA 2011, Brussels, 2011.
  12. Kim, H.-G. and Meissner, C.: Correction of LiDAR measurement error in complex terrain by CFD: Case study of the Yangyang pumped storage plant, Wind Eng., 41, 226–234,
    https://doi.org/10.1177/0309524X17709725, 2017.